Wilcoxon Rank Sum Test

We learned how the sample mean and SD are susceptible to outliers. The t-test is based on these measures and is susceptible as well. The Wilcoxon rank test (equivalent to the Mann-Whitney test) provides an alternative. In the code below, we perform a t-test on data for which the null is true. However, we change one sum observation by mistake in each sample and the values incorrectly entered are different. Here we see that the t-test results in a small p-value, while the Wilcoxon test does not:

set.seed(779) ##779 picked for illustration purposes
N=25
x<- rnorm(N,0,1)
y<- rnorm(N,0,1)

Create outliers:

x[1] <- 5
x[2] <- 7
cat("t-test pval:",t.test(x,y)$p.value)

## t-test pval: 0.04439948

cat("Wilcox test pval:",wilcox.test(x,y)$p.value)

## Wilcox test pval: 0.1310212

The basic idea is to 1) combine all the data, 2) turn the values into ranks, 3) separate them back into their groups, and 4) compute the sum or average rank and perform a test.

library(rafalib)
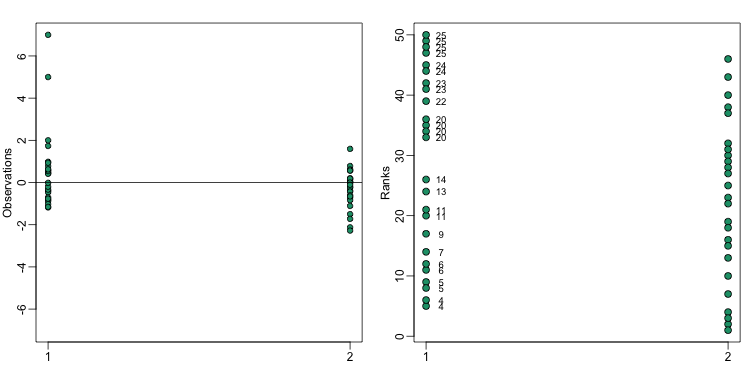
mypar(1,2)

stripchart(list(x,y),vertical=TRUE,ylim=c(-7,7),ylab="Observations",pch=21,bg=1)
abline(h=0)

xrank<-rank(c(x,y))[seq(along=x)]
yrank<-rank(c(x,y))[-seq(along=y)]

stripchart(list(xrank,yrank),vertical=TRUE,ylab="Ranks",pch=21,bg=1,cex=1.25)

ws <- sapply(x,function(z) rank(c(z,y))[1]-1)
text( rep(1.05,length(ws)), xrank, ws, cex=0.8)

W <-sum(ws) 

W is the sum of the ranks for the first group relative to the second group. We can compute an exact p-value for $W$ based on combinatorics. We can also use the CLT since statistical theory tells us that this W is approximated by the normal distribution. We can construct a z-score as follows:

n1<-length(x);n2<-length(y)
Z <- (mean(ws)-n2/2)/ sqrt(n2*(n1+n2+1)/12/n1)
print(Z)

## [1] 1.523124

Here the Z is not large enough to give us a p-value less than 0.05. These are part of the calculations performed by the R function wilcox.test.